强化学习笔记2————蒙地卡罗与时序差分
上一节中我们介绍了马尔科夫链和在强化学习中Q值和V值的定义,那么在实际训练的时候,我们怎么去计算一个节点的Q值或者V值呢,这就要提到著名的蒙地卡罗算法(mc)和时序差分算法(td)
蒙地卡罗
原理
蒙地卡罗的算法原理并不难理解,下面这张图可以很好的概括。
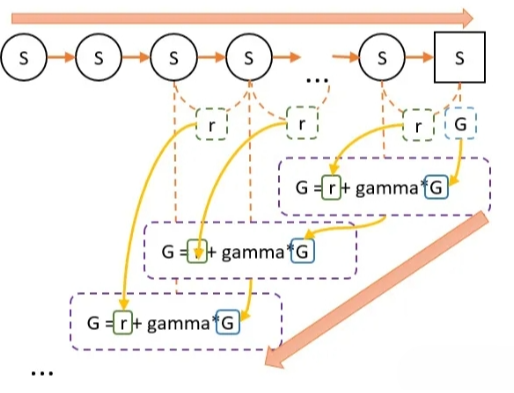
具体来说,蒙地卡罗的算法流程分为以下几个步骤:
- 我们把智能体放到环境的任意状态;
- 从这个状态开始按照策略进行选择动作,并进入新的状态。
- 重复步骤2,直到最终状态;
- 我们从最终状态开始向前回溯:计算每个状态的G值。
- 重复1-4多次,然后平均每个状态的G值,这就是我们需要求的V值。
首先我们要理解每一次我们算的G值的意义。G值的意义在于,在这一次游戏中,某个状态到最终状态的奖励总和(理解时可以忽略折扣值)
- 第一步,我们根据策略往前走,一直走到最后,期间我们什么都不用算,还需要记录每一个状态转移,我们获得多少奖励r即可。
- 第二步,我们从终点往前走,一遍走一遍计算G值。G值等于上一个状态的G值(记作G’),乘以一定的折扣(gamma),再加上r。
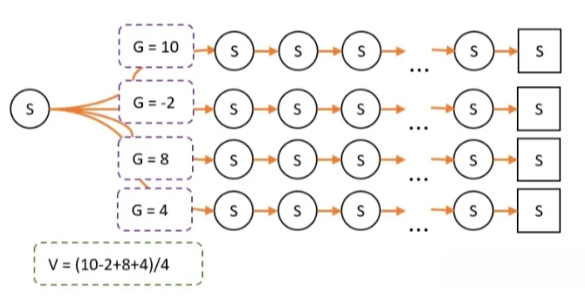
当我们进行多次试验后,我们有可能会经过某个状态多次,通过回溯,也会有多个G值。 重复我们刚才说的,每一个G值,就是每次到最终状态获得的奖励总和。而V值时候某个状态下,我们通过影分身到达最终状态,所有影分身获得的奖励的平均值。
再进一步
蒙地卡罗算法单独拿出来,在强化学习中效率还是比较低的。所以会结合其他的方式进行应用。这些我们会在后面具体算法中讲到。
在这一篇中,希望大家能够理解两点: 1. G的意义:在某个路径上,状态S到最终状态的总收获。 2. V和G的关系:V是G的平均数。
到这里要注意一点:V和策略是相关的,那么在这里怎么体现呢?这个非常重要,因为在PPO算法中,离线策略就与这个有关。这里可以稍微先说一下。
我们仍以上图为例子,以策略A进行游戏。其中有100次经过S点,经过S点后有4条路径到达最终状态,计算G值和每条路径次数分别如下:
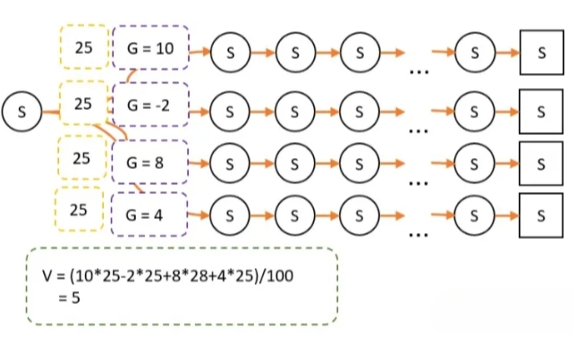
策略A采用平均策略,这时候 V = 5。
现在我们采用策略B,由于策略改变,经过某条路径的概率就会产生变化。因此最终试验经过的次数就不一样了。
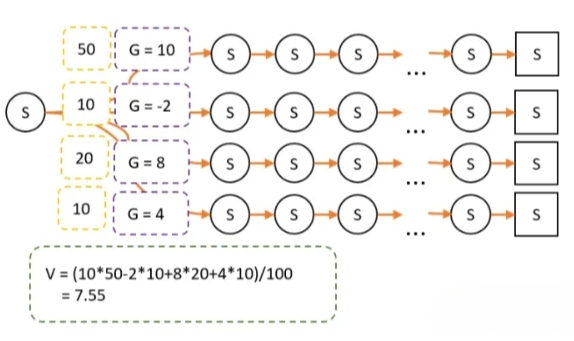
最终计算的 V = 7.55。
蒙地卡罗的缺陷
在实际引用中,蒙地卡罗虽然比动态规划消耗要少一点;而且并不需要知道整个环境模型。
但蒙地卡罗有一个比较大的缺点,就是每一次游戏,都需要先从头走到尾,再进行回溯更新。如果最终状态很难达到,那小猴子可能每一次都要转很久很久才能更新一次G值。
时序差分算法
TD和MC的比较
TD算法对蒙地卡罗(MC)进行了改进。 1. 和蒙地卡罗(MC)不同:TD算法只需要走N步。就可以开始回溯更新。 2. 和蒙地卡罗(MC)一样:小猴需要先走N步,每经过一个状态,把奖励记录下来。然后开始回溯。 3. 那么,状态的V值怎么算呢?其实和蒙地卡罗一样,我们就假设N步之后,就到达了最终状态了。 - 假设“最终状态”上我们之前没有走过,所以这个状态上的纸是空白的。这个时候我们就当这个状态为0. - 假设“最终状态”上我们已经走过了,这个状态的V值,就是当前值。然后我们开始回溯。
TD原理的直观理解
我们可以把TD看成是这样一种情况:
我们从A状态,经过1步,到B状态。我们什么都不管就当B状态是最终状态了。
但B状态本身就带有一定的价值,也就是V值。其意义就是从B状态到最终状态的总价值期望。(这一点在之前Q值和V值那篇已经说明过,就不在赘述了。)
我们假设B状态的V值是对的,那么,通过回溯计算,我们就能知道A状态的更新目标了。
这就有点像从山顶像知道要下山的路有多长。 MC能直接走一趟,看一下到底有多远。 TD则轻巧一点,先走一段路看一下,看一下有没有路牌指示到山脚还有多远。如果有,那么就把刚刚走的那段路加上路牌指示到山脚的距离相加即可。 但又同学可能会问,在一开始,我们根本没有路牌呀,所以也不知道到底到山脚有多远。 没错,这是对的。但当我们走很多次的时候,路牌系统就能慢慢建立起来。 例如第一次,只有到了山脚,我才知道山脚前一站离山脚的的真实距离。于是我更新了山脚前一站的路牌。第二次,我在山脚前一站路就能看到路牌,所以我就可以更新山脚前一站的路牌了…一直到山顶,就这样一直建立整座山的路牌系统。
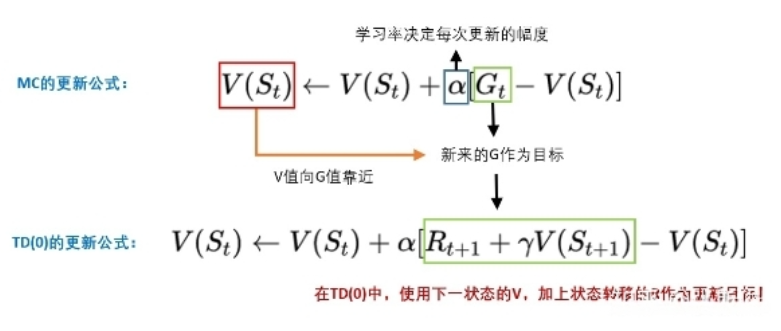
更新公式
刚刚我们对TD有个直观的理解:TD并走走完整段路程,而是半路就截断。用半路的路牌,更新当前的路牌。所以我们只需要把MC的更新目标,改为TD的更新目标即可。在MC,G是更新目标,而在TD,我们只不过把更新目标从G,改成$r+gamma*V$