之前了解了Qlearning的基本思路，在Qlearning中，我们有一个Qtable，记录着在每一个状态下，各个动作的Q值。Qtable的作用是当我们输入状态S，我们通过查表返回能够获得最大Q值的动作A。也就是我们需要找一个S-A的对应关系。这种方式很适合格子游戏。因为格子游戏中的每一个格子就是一个状态，但在现实生活中，很多状态并不是离散而是连续的。而且当例如在GYM中经典的CartPole游戏，杆子的角度是连续而不是离散的。在Atari游戏中，状态也是连续的。遇到这些情况，Qtable就没有办法解决。我们刚才说了Qtable的作用就是找一个S-A的对应关系。所以我们就可以用一个函数F表示，我们有F(S) = A。这样我们就可以不用查表了，而且还有个好处，函数允许连续状态的表示。这时候，我们深度神经网络就可以派上用场了。因为我们之前说过，神经网络就可以看成一个万能的函数。这个万能函数接受输入一个状态S，它能告诉我，每个动作的Q值是怎样的。

Deep Qlearning

模型结构

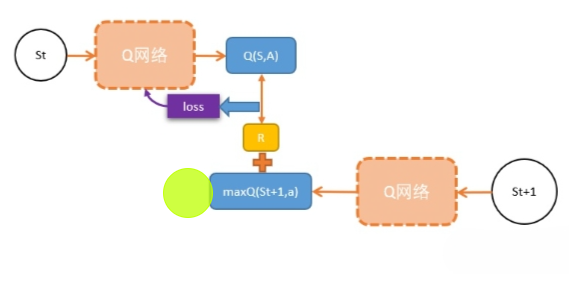
假设我们需要更新当前状态St下的某动作A的Q值：Q(S,A),我们可以这样做： 1. 执行A，往前一步，到达St+1; 2. 把St+1输入Q网络，计算St+1下所有动作的Q值； 3. 获得最大的Q值加上奖励R作为更新目标； 4. 计算损失 - Q(S,A)相当于有监督学习中的logits - maxQ(St+1) + R 相当于有监督学习中的lables - 用mse函数，得出两者的loss 5. 用loss更新Q网络。

也就是，我们用Q网络估算出来的两个相邻状态的Q值，他们之间的距离，就是一个r的距离。

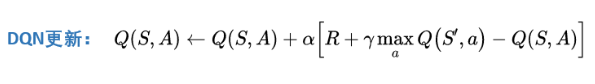
训练方式

假设我们需要更新s状态的Q值(allQ),allQ是所有动作的Q值[0.1 0.2 0.1 0.6]，分别代表采取动作上、下、左、右。如果我们用贪婪算法，我们会选出的动作是【下】，因为【下】的Q值最大。但很遗憾，由于我们采用epsilon-greedy，这次我们随机并随机到a是动作2【右】，然后我们求出下一状态s1的Q值(Q1),现在我们有下图：

其中，绿色格子代表动作a。蓝色格子是Q1的最大值，也就是maxQ1 = np.max(Q1)。现在我们需要构造target，因此我们把allQ先复制给targetQ。然后把r + lambd * maxQ1复制给targetQ中对应a的位置。

所以，我们现在有allQ向targetQ更新：

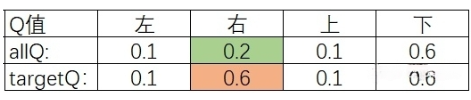
我们可视化一下，就可以看到Q网络的调整方向：动作1,3,4将会不变，而将会把动作2的Q值向targetQ的动作2方向靠近。

小结

其实DQN就是Qlearning扔掉Qtable，换上深度神经网络。
我们知道，解决连续型问题，如果表格不能表示，就用函数，而最好的函数就是深度神经网络。
和有监督学习不同，深度强化学习中，我们需要自己找更新目标。通常在马尔科夫链体系下，两个相邻状态状态差一个奖励r经常能被利用。

Policy Gradient

从蒙多卡洛（MC）到时序差分（TD）,再到Qlearning，最后发展到DQN，其实我们都是在想办法计算在不同我们在马尔科夫状态链每个状态下的Q值和V值，然后在旋转能够使Q值或者V值最大的方向去执行，但是细想一下，我们在做决策时真的需要这样去计算吗，为什么不能直接告诉我在某个状态下该往哪个方向去决策呢？策略梯度(Policy Gradient)就是这样一直方法。

如果说DQN是一个TD+神经网络的算法，那么PG是一个蒙地卡罗+神经网络的算法。在神经网络出现之前，当我们遇到非常复杂的情况时，我们很难描述，我们遇到每一种状态应该如何应对。但现在我们有了神经网络这么强大的武器，我们就可以用一个magic函数直接代替我们想要努力描述的规则。我们用 $\pi$表示策略，也就是动作的分布。那么我们期望有这么一个magic函数，当我输入state的时候，他能输出$\pi_i$，告诉智能体这个状态，应该如何应对：$\pi_i$= magic(state)。如果智能体的动作是对的，那么就让这个动作获得更多被选择的几率；相反，如果这个动作是错的，那么这个动作被选择的几率将会减少。问题在于，我们怎么衡量对和错呢？PG的想法非常简单粗暴：蒙地卡罗的G值！

我们先来复习一下蒙地卡罗:我们从某个state出发，然后一直走，直到最终状态。然后我们从最终状态原路返回，对每个状态评估G值。所以G值能够表示在策略下，智能体选择的这条路径的好坏。

算法流程

我们先用数字，直观感受一下PG算法。从某个state出发，可以采取三个动作。假设当前智能体对这一无所知，那么，可能采取平均策略 $\pi_0$ = [33%,33%,33%]。智能体出发，选择动作A，到达最终状态后开始回溯，计算得到 G = 1。

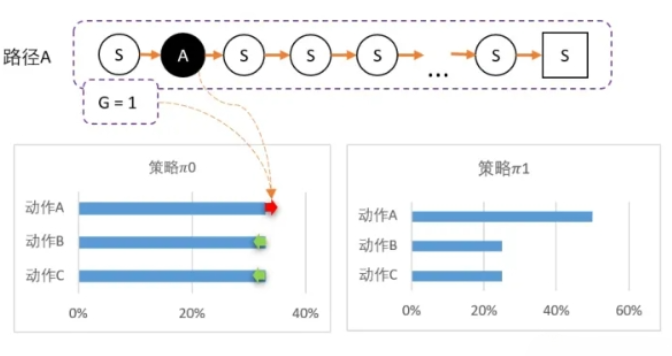
我们可以更新策略，因为该路径选择了A而产生的，并获得G = 1；因此我们要更新策略：让A的概率提升，相对地，BC的概率就会降低。计算得新策略为： $\pi_1$ = [50%,25%,25%]，虽然B概率比较低，但仍然有可能被选中。第二轮刚好选中B。智能体选择了B，到达最终状态后回溯，计算得到 G = -1。

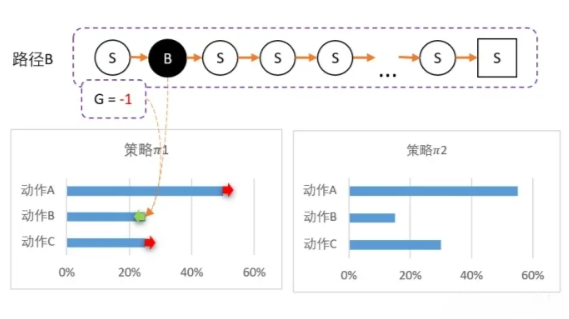
所以我们对B动作的评价比较低，并且希望以后会少点选择B，因此我们要降低B选择的概率，而相对地，AC的选择将会提高。计算得新策略为： $\pi_2$ = [55%,15%,30%]，最后随机到C，回溯计算后，计算得G = 5。

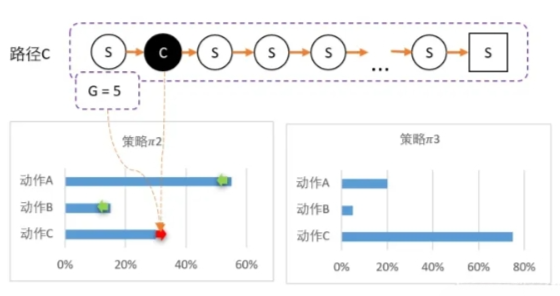
C比A还要多得多。因此这一次更新，C的概率需要大幅提升，相对地，AB概率降低。 $\pi_3$ = [20%,5%,75%]

训练过程

我们以某一个状态为例，在某个状态下，通过网络得到的预测值$y^*$，真实值$y$，G值,如下图

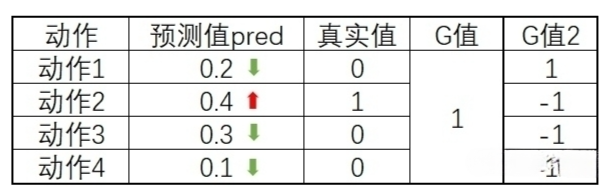
我们可以把这个过程想象成一个分类任务。在训练的时候，只有真实值为1，其他为0。所以动作1,3,4的概率将会向0靠，也就是减少。而动作2的概率将会向1靠，也就是说会有所提升。我们可以使用交叉熵对这个分布进行调整。

这里的G值的作用类似于权重，在代码中的实现方式为：

1	loss = tf.reduce_mean(neg_log_prob * G)

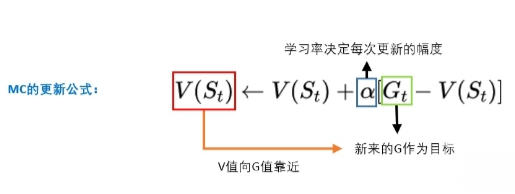
当G值调整大小的时候，相当于每次训练幅度进行调整。例如G值为2，那么调整的幅度将会是1的两倍。如果G值是一个负数呢，那么相当于我们进行反向的调整。如下图，如果G值为-1，那么说明选择动作2并不是一个“明智”的动作。于是我们让这个动作2的预测值降低，相当于“远离”真实值1。而其他动作的概率有所提升，相当于“远离”真实值0。

总结一下：1、通过网络，求出预测值pre的分布。 2、和真实值action进行比较，求得neg_log_prob 3、最终求得neg_log_prob乘以G值，求得loss

小结

PG用一个全新的思路解决了问题。但实际效果显得不太稳定，在某些环境下学习较为困难。另外由于采用了MC的方式，需要走到最终状态才能进行更新，而且只能进行一次更新，这也是PG算法的效率不高的原因。